The Higgs boson and the top quark
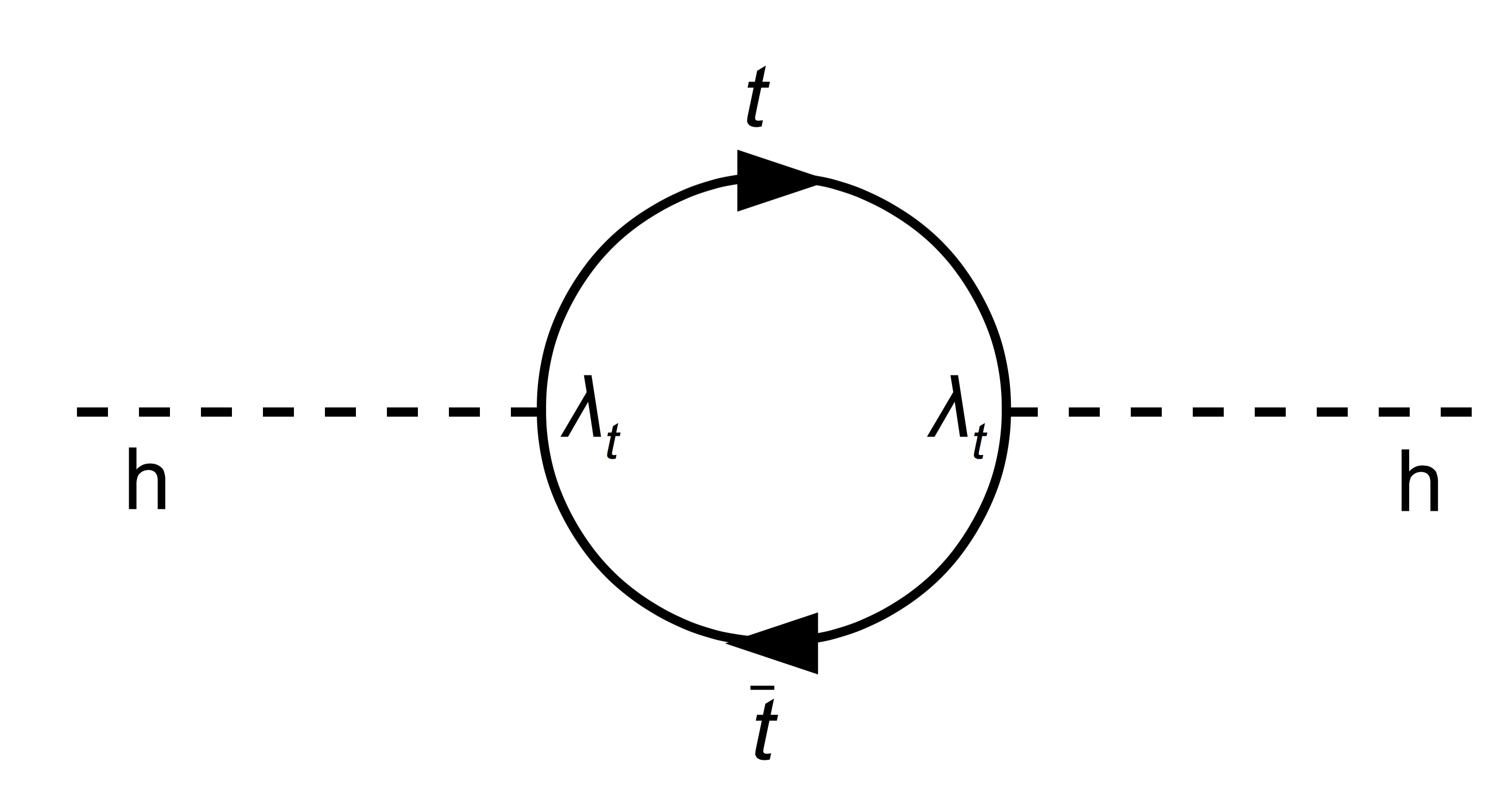
Figure 1: Loop corrections to the Higgs mass
are dominated by top quark loops.
The discovery of a Higgs boson at a mass of about 125 GeV in 2012 in proton-proton collision data provided by the Large Hadron Collider (LHC) answers the question of how elementary particles acquire mass, via the Higgs mechanism. The top quark is the heaviest elementary particle discovered so far, and hence a very special quark. It has a mass of about 173 GeV, which almost corresponds to the mass of a gold atom. In a future theory of particle physics, based on our current best theoretical model (standard model, SM), the mass of the Higgs boson gets affected by loop corrections, which are dominated by the top quark.
Figure 1 shows the loop corrections to the Higgs mass due to the top quark. Since the momentum of the top quark is not limited in those loops, the corrections to the Higgs mass are huge:
In fact they correct the Higgs mass to a mass of about 1019 GeV (aka Planck scale), in strong disagreement to the experimental data. This shortcoming is known as the hierarchy problem and various beyond the SM solutions exist, and many predict a top quark partner to cancel the corrections to the Higgs mass exactly.
![]()
The Jung research group focuses on the question of how the mass of the Higgs boson is stabilized, or to put it in more general words: how the electroweak scale is stabilized. A potential top quark partner represents a viable solution for this fundamental problem and the Jung group is in particular involved in high precision measurements in the top quark sector to identify potential contributions from non-SM sources. More details can be found under the following link: Research Activities.
The electroweak vacuum stability
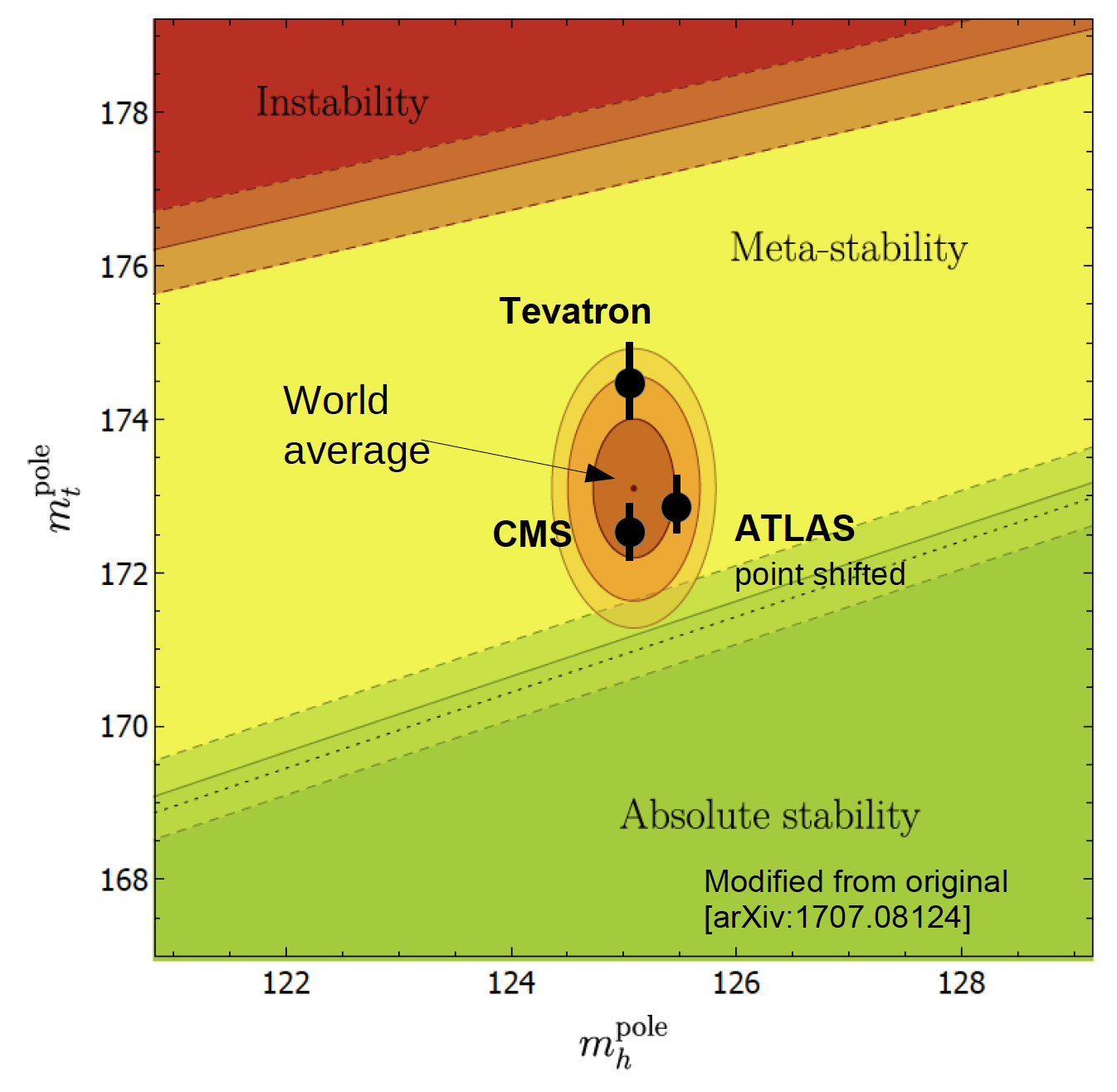
Figure 2: Results from the Tevatron and LHC
in the m(higgs) versus m(top) plane on top
of the instable, meta-stable, and stable
regions of the electroweak vacuum stability.
The discovery of a Higgs boson in 2012 at the LHC provides a crucial mile stone and success for the SM. The observation of the Higgs Boson confirmed for the first time, that the SM - our current best theoretical prescription for elementary particles - is consistent up to highest energy scales. Hence, we can check the dependence of the Higgs quartic self-coupling Ⲗ on the energy scale. For reasons already discussed the top quark has a significant impact on Ⲗ and for top quark masses of about 175 GeV causes Ⲗ to be negative. However, only a positive Ⲗ preserves the mexican-hat shaped potential, which is one of the crucial ingredients for the Higgs mechanism to work as expected.
Latest measurements of the top quark mass by LHC and Tevatron experiments have reached a precision significantly smaller than 1 GeV. Figure 2 shows the latest measurements in the m(higgs) versus m(top) plane on top of the instable, meta-stable, and stable regions of the electroweak vacuum stability. More details can be found under the following link: Research Activities and in the selected list of the Jung groups publication list at the following link: Publications.
Properties of the Top quark
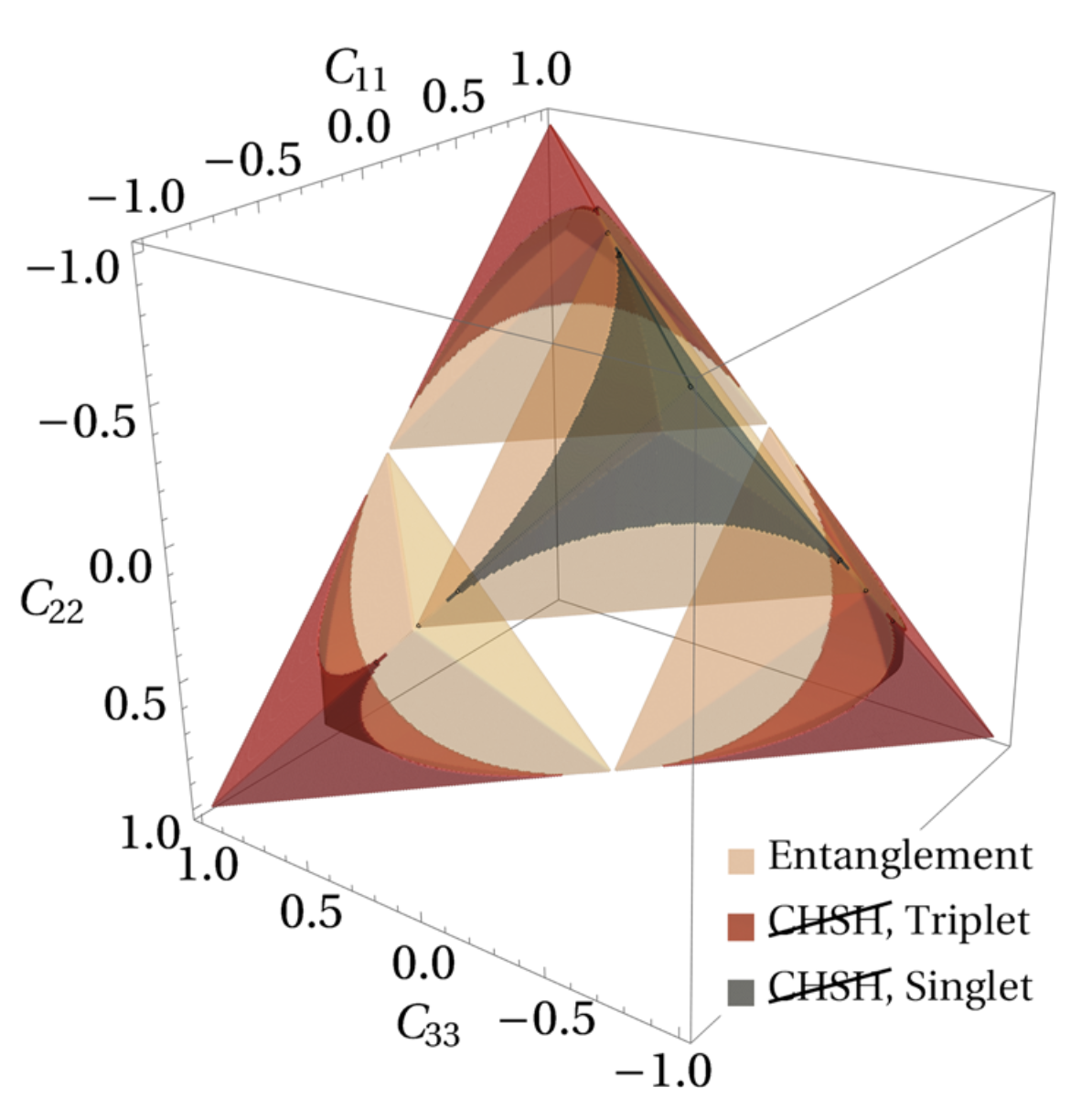
Figure 3: Regions along the three directions
of C where the density matrix is entangled
and where Bell's inequality is violated
[Eur. Phys. J. C (2022) 82:285].
The analysis of the double-differential cross section as a function of the angles of the decay leptons allows to measure the correlation of the spins of the top quark, as well as the polarization of top quarks (expected to be 0 in the SM). More information on measurements of the spin density matrix can be found following this link: Research Activities. Another exciting measurement is presented by the unique access to bare quarks in top-anti-top quark pair production. Namely, a measurement of the density matrix of the spin of a top-anti-top quark pair can be expressed as:
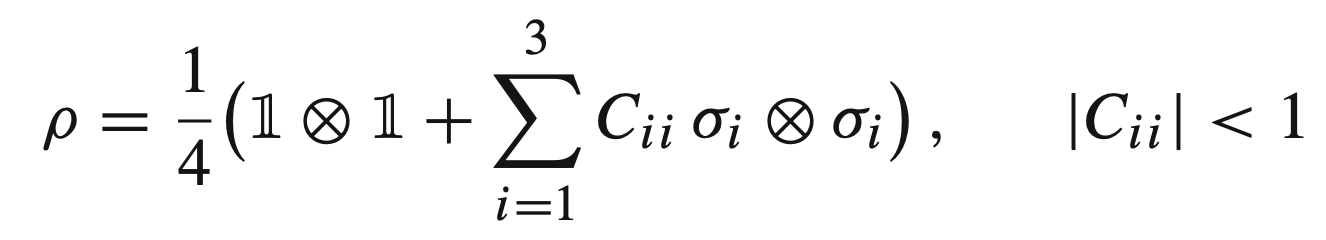
Quantum tomography is an exciting new window into the inner and fundamental workings of quantum mechanics. Loose connections to a variety of quantum computing related topics exist, such as vertex finding at the high-luminosity LHC, applications of machine learning executed on quantum computers or more general the devleopment of quantum algorithms. More information of the activities of the Jung group in the area of Quantum Computing can be found here: Quantum Algorithm Development.
This research is supported by:



Latest News
- Latest CMS News
- Observation of tt Entanglement
- DOE CMS upgrade award
- AirForce Phase III award
- DOE awards AI grant
- CMS Gold award
- Enormous Carbon Fiber prototype
- CMS upgrades funded
- Ramdas Award 2019
- New physics ?
- Summer 2018 UG exchange
- CMS phase II pixel upgrade workshop @Purdue
- Huffington Post: A new inner detector installed for CERN CMS experiment
- All News