Purdue professor uses a new geometric framework to study quantum dynamics
2021-01-04
Writer(s): Cheryl Pierce
A hyperbolic geometry is being used to study and relate two types of quantum dynamics which were previously considered separately. Dr. Qi Zhou, Associate Professor of Physics and Astronomy at Purdue University, and his team recently discovered that a new geometric framework can be used to understand and control quantum dynamics of ultracold atoms, as reported in two recent publications in Physical Review Letters. Dr. Zhou’s graduate students, Changyuan Lyu and Chenwei Lv, are the first authors of these two publications, respectively. Prof. Ren Zhang from Xi’an Jiaotong University is the co-first author of one of the publications.
Two Recent publications in Physical Review Letters
Prof. Zhou's group recently found something more than meets the eye with how quantum dynamics of Bose-Einstein Condensates fit into a geometric pattern. A Bose-Einstein Condensate cannot be found easily in nature. Physicists need to cool a gas of bosons at low densities to temperatures very close to absolute zero, down to a few tens of nano Kelvin, where quantum effects become profound. Zhou’s team researches this field of ultracold atoms, a subarea in physics, by studying behaviors of the atoms and molecules in such a low temperature regime.
“Many microscopic parameters in Bose-Einstein Condensates are highly controllable,” says Zhou. “They thus provide physicists an extremely rich playground to explore quantum dynamics in a many-body system, among many other things. In our daily life, we are familiar with dynamics of classical systems. For instance, if a pendulum is displaced away from where it rests, it will oscillate back and forth."
Stirring quantum systems, which consist of many particles, creates much more intriguing phenomena. The mutual interactions between particles lead to collective excitations unattainable by any individual particles. Such quantum many-body dynamics have attracted physicists' interest for many decades.
“Two prototypical types of many-body dynamics have been studied extensively in the field of ultracold atoms,” explains Zhou. "The first type of dynamics arises when suddenly changing the interaction strength in a Bose-Einstein condensate. Following this disturbance, the occupation numbers of all quantum states shall be modified. Under certain conditions, the occupation numbers of some quantum states will grow without an upper bound, a phenomenon known as the dynamical instability that occurs in a broad range of non-linear systems. The other type is the breathing mode. Tuning the strength of the external trapping potential, which is typically a harmonic trap, to a new value, the condensate begins to vibrate like a lung. The periodically modulated size of the condensate earns it the name of ‘breather’."
Whereas both types of dynamics have been well studied, the new geometric framework introduced by Zhou’s team unfolds a hyperbolic geometry hidden in these phenomena that had been believed to be well understood. The hyperbolic geometry, which seems to be a totally unrelated concept, underlies both the dynamical instability and the breathers. Both of them can be mapped to paths on Poincare disks, a curved space in which the distance is measured in a distinct means compared to the metric in our daily life.
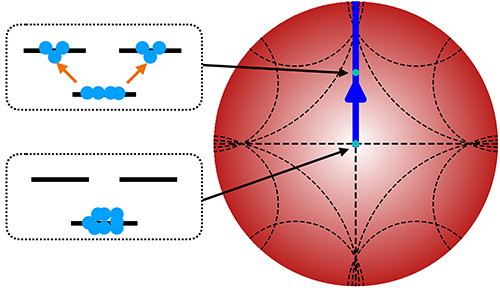
“On Poincare disks, the shortest distance between two points may not be a straight line any longer,” says Zhou. “In such curved spaces, some paths do not have a turning point and move towards infinity. As explained by one of the two publications, this is precisely a geometric interpretation of the dynamical instability. Some other paths, however, return to their starting points after some time. Breathers fall into this category, as shown in the other publication."
“The geometrization of quantum dynamics provides not only a new angle to understand many-body systems but also a bridge to connect different disciplines.” Says Lyu. “By correlating fundamental quantities including the time, the length, and the temperature, this method shows that the dynamical instability has a deep connection to the so-called thermofield double state, which plays a critical role in understanding the connections between quantum mechanics and gravity."
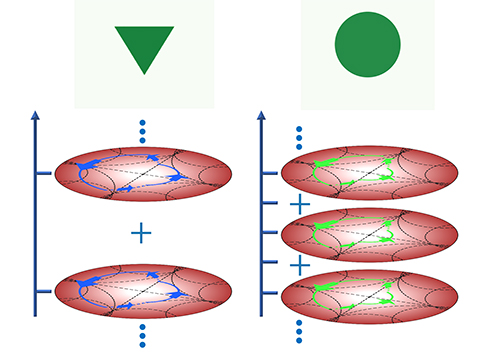
In addition, this geometric approach explains a mystery found in a recent experiment by the group. Although these extraordinary behaviors of breathers were observed in an experiment last year, there lacked a theoretical explanation.
“Unexpectedly, the frequency of breathers depends on their initial shapes,” says Lv. "Whereas some breathers agree well with the textbook results, some others have distinct frequencies. To make it more strange, certain breathers do not show regular periodicities. The geometry offers a natural understanding of this mystery. Some breathers require the superposition of multiple Poincare disks and paths on different Poincare disks may acquire distinct dynamical phases after returning to the starting point. Such interferences, a unique feature of quantum mechanics, change the periodicities of breathers or even destroy their periodic oscillations.”
It is not accidental that both the dynamical instability and the breathers are governed by the same hyperbolic geometry. A fundamental symmetry in group theory exists in both cases, each merely corresponding to a different representation of the same SU(1,1) group.
“Understanding the underlying geometry and symmetry will also help us to design new tools to manipulate the quantum dynamics”, says Zhang. "For instance, it leads to an elegant echo to reverse quantum dynamics of a broad range of quantum systems that also have the same SU(1,1) symmetry. It is known that the well-established spin echo is based on the SU(2) group. We believe that the SU(1,1) echo we proposed will also have a wide range of applications."
Zhou’s team will continue to work on this geometric discovery and use it to develop new means to understanding and manipulating quantum dynamics of ultracold atoms.
“The current discoveries are just a tip of the iceberg,” says Zhou. “We will continue our journey to explore the deep connections between dynamics, geometry, and symmetry.”