Demos: 1S-31 Motion Under Hooke's Law (SHM)

Several springs of different stiffness are available. The differences involve the length, material and/or diameter. The demonstration shows the dependence of the period of oscillation on (a) the force constant. (b) the attached mass M and (c) the mass of the spring. The period is independent of the amplitude.
Note: If the mass, m, of the spring is significant compared with the attached mass, M, a correction must be made for the period, which turns out to be adding 1/3 the mass of the spring to the attached mass, i.e.
Directions: To illustrate the role of the force constant, choose two springs of the same length, one having considerably more stiffness than the other. To illustrate that the force constant is not just the property of the material in the spring, select the spring that has a horizontal bar at its center. First attach the spring to the stand at its end point and allow it to oscillate. Then attach it at the “bar” and allow it oscillate again. This is equivalent to two identical springs except for length. To see the effect of amplitude, pull the weight down different distances and check the period. If you wish, you can use a timer to determine the actual periods in each case.
Suggestions for Presentation: When discussing the force constant (sometimes referred to as the “spring constant”), be aware that many students believe this constant to be simply a property of the spring, namely its composition, or stiffness. Ask what would happen to the period if you had identical springs except that one is longer than the other.
If you wish to pursue the spring mass correction, you might actually determine the period of a system for which the spring mass is comparable to the attached mass. Use the standard expression to check your results. They will be considerably different (see below). Discuss how this might have occurred. One clue is take a spring without a mass attached and show that it has its own period of oscillation. How can this be reconciled?
Example: m (brass spring) = 0.165 kg; k = 10 N/m; M = 0.15 kg
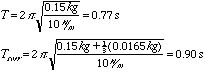
Applications: Resonant frequencies of a variety of oscillating systems.
Last Updated: Nov 30, 2023 11:25 AM