Demos: 1S-03 Meter Stick Pendulum

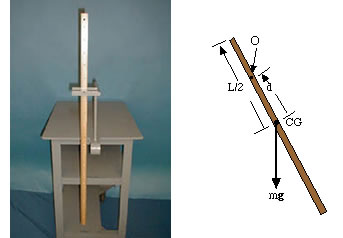
A meter stick can be suspended from a number of points, located at a distance d_i from the center of gravity. The period of this physical pendulum is



If the meter stick is suspended at point O, as illustrated, the rotational inertia is





If we let d = x (L/2), where 0 £ x £ 1, then



If the stick is suspended at its center (x = 0), the period becomes “infinite.” If suspended at its end, the period is



which is equivalent to a simple pendulum of length 2/3 L. NOTE: If you start from the end, the period at first gets smaller, then starts to get larger, as it must, when x approaches zero. The minimum occurs at about x = 0.6.

Directions: Suspend the meter stick from various points above the center of gravity and note the changes in period. If you wish, you can time, say, ten periods and make a semi-quantitative comparison. If all parameters are specified, you can carefully time the period and compare it with the results derived above.

Suggestions for Presentation: Begin by asking what the period of a meter stick should be if suspended at its end. Some students may think of a simple pendulum and simply use the length L to compute the period. Show how the results are not the same. OR, to follow up on the simple pendulum misconception, ask what the period will be if the meter stick is suspended at its center (L/2). If one uses the simple pendulum formula, a small finite value will be obtained. If you actually suspend it from the center, one can see that period is very long (infinite). It can be helpful to show a simple pendulum of the predicted length having the same period.

Applications: Pendulum clocks.

Add to Cart | View Cart