Demos: 1S-02 Compound Pendulum

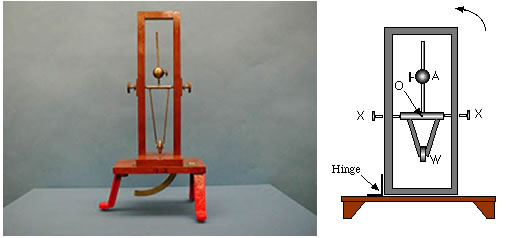
The pendulum oscillates about the axis X-X in a plane perpendicular to X-X. The weight W is fixed, whereas the weight A can slide up and down the shaft, altering the rotational inertia. The period of the pendulum about O is found from:



where d is the distance to the center of gravity of A and W (assuming the other masses to be negligible). If A and W are also approximated as point masses, then



The center of gravity is located, relative to O,



This leads to



Note that if M_A is zero, we have the result for a simple pendulum. If M_A = M_W and d_A = d_W, the period of the pendulum is indefinitely large, as expected.

If the entire mechanism is tilted about the hinge through an angle q, the factor g becomes gcosq and the period will increase (Mach’s Pendulum).

Directions: For a qualitative approach to the demonstration, simply move the sliding mass to various positions and show the positional dependence. In particular, if the mass A is placed such that it is located at the center of gravity, the period will become indefinitely large (infinite). If you wish to perform a quantitative analysis, careful measurements must be made of the distances. (You could measure g if all other parameters are known.)

For the “Mach Pendulum,” leave the masses in position and lift the apparatus to some intermediate angle to show that the period diminishes with q.

Suggestions for Presentation: See Directions above.

Applications: A variant of the Mach Pendulum was used in astronaut training years ago. The astronaut trainee was attached by harness to a long rope. He moved about on a ramp inclined at an angle such that the component of g along the slope was 1/6 that of the Earth. In some ways, the astronaut was able to simulate movement on the moon.

Add to Cart | View Cart