Demos: 1Q-04 Translation with Rolling

A collection of disks and hoops, of different radii and different masses, are allowed to roll from rest without slipping down an inclined plane. It is shown that the one that reaches the bottom first depends not on the mass or radius, but on the shape. To illustrate this further, a wooden disk, clad with a metal ring, rolls down faster than the hoop but slower than the wooden disk.

That the speed at the bottom is independent of shape, consider a hoop and a disk rolling down the incline together. Conservation of mechanical energy for the disk (I = 1/2 MR²) gives us:



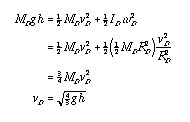
Note that the speed at the bottom depends neither on the radius nor the mass, but rather on the shape. Doing the same analysis for the hoop (I = MR²), we get



and we see that the disk rolls faster and thus reaches the bottom first.

Directions: A rubber strip placed at the top of the ramp insures that the contact points of each object are at the same height initially. Pulling the strip out allows the two objects to start simultaneously. Begin with a wooden disk and a metal hoop of the same radius. Then to show that the radius doesn’t matter, choose a large disk and a small hoop, giving the same result. Finally, place the hoop, the wooden disk clad with the metal ring and the wooden disk together at the top, in that order. Release them and watch the order of arrival at the bottom.

Suggestions for Presentation: Ask if the speed at which the objects reach the bottom depends on the mass or radius. (Since I is proportional to MR², the answer will likely be yes.) Try different masses and radii and show that these variables are not important.

Note: These results are true ONLY if the radius used in the rotational inertia calculation is the same as the “rolling radius.” For example, if you use an annular cylinder, there are two radii involved.

As an interesting sidelight, ask which would go higher up the plane, a hoop or a disk, if both have the same initial translational speed before encountering the incline.

Applications: None that are apparent.

Add to Cart | View Cart