Demos: 1Q-03 Uniform Angular Acceleration/Non-Uniform Angular Acceleration

A large massive flywheel, having a smaller radius pulley rigidly attached, is rotated by means of the tension force in a string wrapped around the pulley. The tension is created by means of a weight hanging from the string after it passes over another isolated pulley, as shown in the picture. Since the mass of the string is negligible, the torque produced by the tension force is constant. If the radius of the attached pulley is r, the rotational inertia of the disk is I, and the hanging weight has mass m, then the angular acceleration is found by



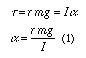
and since all the terms on the right are constant, the angular acceleration is constant. It can, in fact, be measured. The falling weight moves through a distance s in time t:



The time t can be obtained by placing photogate timers a known distance apart on the vertical post. Then make use of the fact that a = a / r.

One can test this against a “theoretical result” if the mass of the large disk and its radius are known. Assume the attached pulley mass to be negligible and use , where R is the radius of the large disk and M is its mass. Use Eq (1) above to compute a.

Directions: With the string wrapped securely around the attached pulley, pass one end over the pulley on the post. Attach different weights to show the effect on the acceleration.

Suggestions for Presentation: Make sure the students notice that the “torque r” and the “rotational inertia R” are different. You might also have them think about the effect of reducing r to smaller and smaller values.

Applications: An indirect application is to flywheels. For example, you might give some light impulsive “yanks” on the hanging weight as it falls and see that the acceleration of the large disk is still relatively uniform, i.e. the large rotational inertia smooths out the variations in torque.

To demonstrate Non-Uniform Angular Acceleration: A chain of very small mass (when compared to the fly wheel) is wrapped around a metal cylinder (flywheel) and passed over a pulley, where a small amount initially hangs vertically. The weight of the hanging portion creates a tension in the chain that, in turn, exerts a torque about the central axis of the disk. The torque uniformly increases as more of the change passes over the pulley. Therefore the angular acceleration also increases uniformly, since the rotational inertia remains constant.

Add to Cart | View Cart