Demos: 1Q-01 Rotational Motion

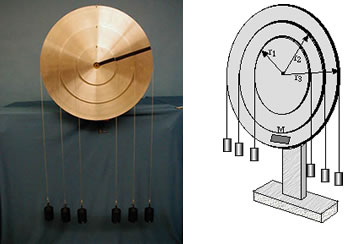
Three pulleys of different diameters, rigidly attached together concentrically, turn together about a central axis. The system is loaded with an off-axis weight M, which tends to stay down. Pairs of identical weights attached to appropriate lengths of wires can be strung over the pulleys such that at equilibrium (M at its lowest position) they remain at the same height. (The wires are fixed on the rim at their centers so they do not slip.)

When the system is rotated (by hand) through an angle , the weights are displaced through vertical distances, r₁, r₂ and r₃, respectively. When the system is released from this position, all three pulleys rotate with the same angular speed, , but the weights move with different linear speeds, v_i = r_i , and they all reach the equilibrium position at the same time. This is a clear demonstration that the tangential speed is proportional to r.

Directions: Make sure the cables are placed securely in the grooves of the pulleys. Slowly rotate the system through an angle of 30° or so and hold it in this position. Point out the differences in heights of the weights, indicating that they have moved different vertical distances. Rather than release the weights, which would make them oscillate about the equilibrium position, you can slowly bring the system back to the equilibrium position, allowing the students to see how the different weights travel at different tangential speeds.

Suggestions for Presentation: Make a clear case for the fact that the pulleys are all moving with the same angular speed. Then ask how the tangential speed is related to this

Applications: Refer to a Merry-Go-Round, where the person on the outside moves faster tangentially. Also, when a lever is pivoted about its fulcrum, the ends move through a greater vertical distance than the parts nearer the fulcrum.

Add to Cart | View Cart