Demos: 1M-10 Loop-the-Loop

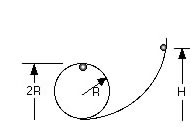
This demonstration is an illustration of the classic problem usually given in physics texts, namely, what speed must a ball have at the bottom of a circular loop to just make it around the loop without falling off? The heavy steel ball is released on the higher arm of a grooved track (friction is reduced significantly). The ball has kinetic energy at the bottom of the circular loop and this energy is transformed partially into potential energy as it climbs back up the ramp. If the ball is to just reach the top of the ramp and not fall off, its speed must be such that the only force keeping it in a circular path is gravity. From earlier studies of circular motion, we know this will happen when v² =gR. Thus the height from which the ball is started is given by



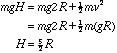
Directions: Place the ball on the ramp at various locations and determine what happens when it enters the loop.

Suggestions for presentation: A mark is evident on the track where the ball should be placed to just get it to go around without falling off. Start with the ball ABOVE this point and show it goes around the loop. Repeat a few times, each time bringing the ball closer to the “magic” height. Then start lower than this and the ball will fall from the loop. You might wish to confirm the height of 5/2 R with a meter stick and point out that friction isn’t entirely negligible here so the starting point for no drop-off is a bit higher than predicted.

Applications: Relate this demo to such things as roller coasters and stunt riders in circular cages. Roller coaster cars always start at points higher than those of other parts of the track. How does the roller coaster have built-in safety factors in case the speed around the loop isn’t fast enough?

Add to Cart | View Cart