Demos: 1M-08 Galileo Track

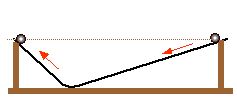A ball moves from rest down a low-friction ramp with a relatively small slope. It then encounters a steeper ramp, but the ball comes to rest at the same elevation that it started from, showing the conservation of mechanical energy.

Directions: Place the ball at the top of the long ramp and release it. It will just about make it to the top of the other end of the ramp. Then show that it doesn’t matter which end you start from.

Suggestions for Presentation: Use the power of suggestion to point out that the ramps are of different length and different slope, so it ought to be difficult to determine where the ball will reach zero speed. Let students guess whether it will go higher or lower than its original height. After performing the demo, ask what conservation of energy has to say about this. If you let the ball oscillate back and forth, it becomes clear that the “final” height in each case is less than the initial height. Ask the students how you might account for this. (Friction really isn’t absent here.)

If you are using this demo at the beginning of the study of the concept of inertia, refer to Galileo’s argument about making the second slope longer and longer until it becomes horizontal. The ball should continue at the same speed “forever.”

Applications: Roller coasters

Add to Cart | View Cart