Demos: 1J-29 Overhanging Blocks
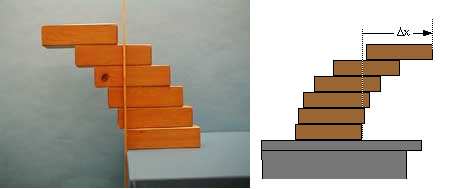
A set of 6 wooden blocks, each 12” long, are stacked in such a way as to achieve the maximum extension of the top block relative to the end of the bottom block. The upper block may actually extend completely beyond the bottom block.
The top block can extend only half way beyond the next lower one, because the CG of the top block cannot extend beyond the edge of the one below it. Then the CG of the two top blocks taken together cannot extend beyond the edge of the third down and so forth. An overhead transparency is available showing the CG points of each combination and how this dictates the stacking arrangement. If you wish to develop this quantitatively, we have for the total extension Dx:
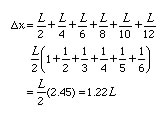
where L = 12”. This is the maximum theoretical extension. In reality, the blocks have to be moved slightly back in each case to avoid tipping, so the total extension will be a little less.
Directions: A line has been marked on each block to show how they are to be stacked. You can tell by the marks the order in which they must be stacked.
Suggestions for Presentation: If the blocks have been pre-stacked by the lecture demo technician, you might ask how the blocks can stay balanced when the top one is beyond the bottom block. Also ask why the extensions get smaller as you move toward the lower block. What if you had an infinite number of boxes. How far would they extend? (An infinite distance) Twenty-five blocks would extend about 2L.
Applications: None that are evident
Last Updated: Nov 30, 2023 11:25 AM