Demos: 1J-26 Disks and Tower

Within the limits of constraints acting on it, an object’s center of gravity in a constant gravitational field tends to be as low as possible. This is illustrated by watching the settling and oscillating of disks whose centers of gravity are away from the central axis.

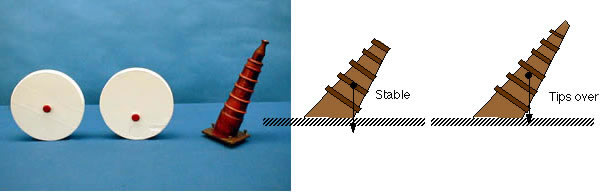
A standing object will be stable against tipping if a vertical line passing through its C of G intersects the base inside the contact points. A leaning tower, consisting of segments that are added one-at-a-time, remains stable until the C of G is high enough to cause its line of action to pass outside the support points, as shown below.

Directions: Stand the disks on the lecture table and do one of two things, or both: With the metal slug in some position other than at the lowest point, release the disk. It will oscillate back and forth about the position in which the mass is lowest. If you roll the disk along the table, it will move with an erratic motion.

Start with the first segment of the tower. (Be sure it is absolutely level, or the last segment won’t tip it.) Keep adding segments carefully. It should remain stable until the last one is added, then it will tip over.

Suggestions for Presentation: You might start with the uniform white disk and place it on the desk, giving it a gentle push. It will roll uniformly. Then take the other white disk and do the same. Why does it behave differently? Then take the unpainted disks that show clearly the C of G shifted away from the center and do the same. They can see how the C of G moves in this case. An interesting demo is to take the white disk having a red knob at its center, face the knob to the students and toss the disk in an arc. (You can toss it to yourself if the arc isn’t too great.) Have the students notice that the disk described a nice smooth motion through the air. Now take the disk having the red knob off-center, but FACE THE OTHER SIDE to the students. This side has a red dot painted in the center, falsely implying that this is the C of G. Toss the disk and it will wobble as it flies through the air. Now show them the other side where the true C of G is indicated by the red knob. If they focus their attention on the knob, they can see that it still traces out a parabolic (smooth) trajectory.

Ask why an object is stable against tipping. Ask why you are stable when you stand normally, but not when you lean too far forward.

Applications: Smooth operation of spinning objects depends on their being balanced. Discuss what this means. For the tower, show a picture of the Leaning Tower of Pisa. Can you estimate where the C of G is?

Add to Cart | View Cart