Demos: 1J-01 Galilean Lever

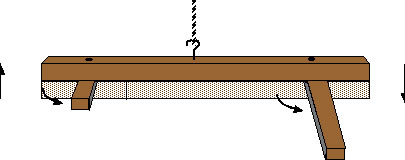
Two 6-foot wooden bars of square cross-section are bolted together at points 6 inches from each end. The lower bar is cut into two pieces one foot from the end. Thus one section of the lower bar is bolted through its center of gravity, whereas the other is not. The entire unit is suspended symmetrically from a hook placed at the center. When the bars are coincident, the system is in horizontal equilibrium. When the shorter bar is rotated by 90°, the system remains in balance because the C of G has not shifted. However, if the longer bar is rotated through 90°, the C of G is shifted and the bar tips dramatically downward at that end.

Directions: Hang the apparatus from the stand. Because of slight asymmetries, weights have been added to one side to insure balance. First rotate the short block and point out that the balance is not affected. Then rotate the longer block and the beam drops dramatically on that end.

Suggestions for Presentation: Point out that the lower bars are capable of being rotated about the bolt. Ask if rotating either one should affect the equilibrium.

As an added bonus, students should be able to locate the position of the C of G of the system after it has become skewed. When the bar reaches its new equilibrium position, the C of G has to be on a line directly below the suspension point.

Applications: Rotating parts on systems will not affect the C of G if the parts are rotated symmetrically about their centers.

Add to Cart | View Cart