Demos: 1D-02 Conical Pendulum

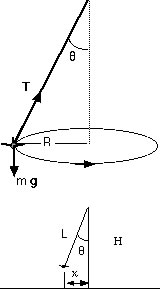A small airplane moves in a horizontal circle at constant speed. Referring to the diagram at the right, we see that



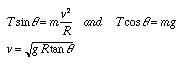
The period of the pendulum is found from



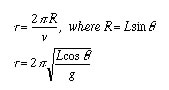
Directions: The airplane is battery-operated and is propelled by a spinning prop. Turn on the switch, hold the plane so that the string makes about a 45° angle with the post. With the plane pointed in the proper direction along the tangent to the path, let it go. It eventually will settle into a smooth circular orbit. To catch the plane, use a net or good timing with your hands!

Suggestions for Presentation: Emphasize that uniform circular motion requires that the NET force be toward the center of the circular path. There may actually be no force in that direction (the case here). Show that the two forces, T and mg, must add as vectors to point toward the center of the circular path.

If you want to calculate the period of the pendulum, you will need to determine the angle. A simple way to do this is to place a vertical rod directly under the path of the plane and determine its distance from the shaft, x (see lower figure). Then use a meter stick to determine the height of the plane’s orbit above the table. We can see that

Applications: Show that this analysis gives the same result as for a banked curve. In that case, there is a normal N from the road rather than a tension force from the string. Also, a real plane uses the lift vector instead of the tension T.

Note: This can also be done with a ball on a string.

Add to Cart | View Cart