Research

Our research group focuses on condensed matter theory, studying the electronic properties of novel materials. Current group interests include high temperature superconductivity, strongly correlated electrons, liquid crystalline phases of electrons, and soft electronic matter.

Funding:

We gratefully acknowledge support from the National Science Foundation, the Department of Energy, the Department of Defense, Research Corporation for Science Advancement, and the Purdue Research Foundation.

Quantum Materials for Neuromorphic Computing

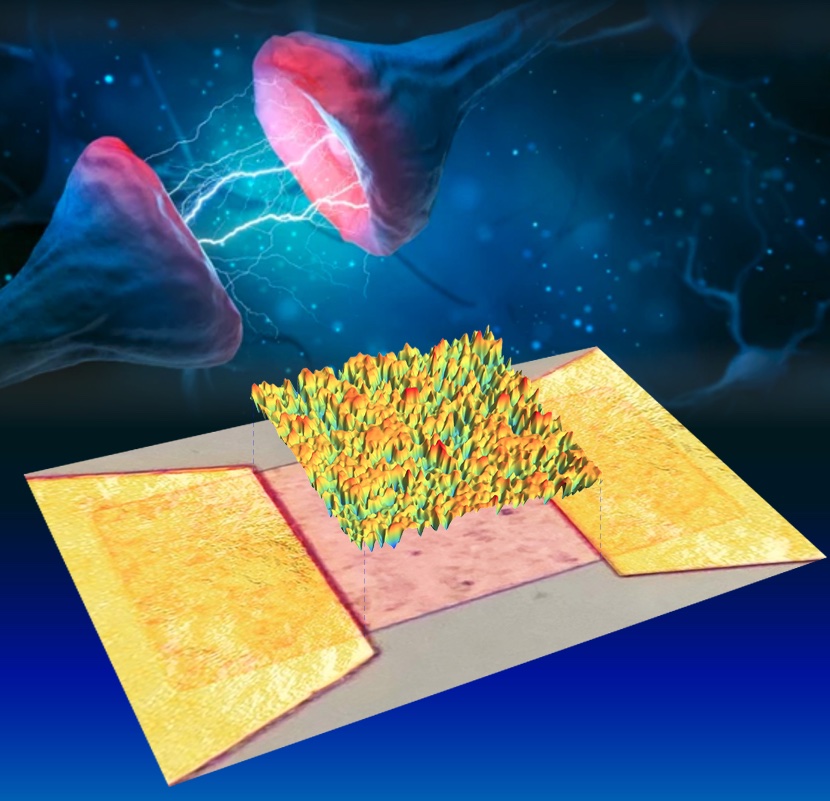
Enabling the next technological leap in computing will require new paradigms in hardware that can support the complexity of tomorrow’s computational advances. Towards this, neuromorphic architectures hold promise for lower energy consumption processors, enhanced computation, fundamentally different computational modes, native learning, and enhanced pattern recognition. Vanadium oxides show tremendous promise for neuromorphic computing because they can be used to make both artificial neurons and synapses. Recently a new type of non-volatile memory, driven by repeated partial temperature cycling through the insulator-to-metal transition, was discovered in vanadium oxides. Spatially resolved optical contrast measurements show that, surprisingly, the repeated advance and retreat of metal and insulator domains causes memory to be accumulated throughout the entirety of the sample, rather than only at the boundaries of domains. The memory appears as shifts in the local temperature at which the material transitions from insulator to metal upon heating, or from metal to insulator upon cooling. The image, derived from optical microscopy, shows the changes in transition temperature in a 28μm X 33μm film of VO2. We propose that these changes in the local transition temperature accumulate due to the preferential diffusion of point defects into the metallic domains that are interwoven through the insulator as the material is cycled partway through the transition.

S. Basak, Y. Sun, M. Alzate Banguero, P. Salev, I. K. Schuller, L. Aigouy, E. W. Carlson, A. Zimmers, “Spatially Distributed Ramp Reversal Memory in VO2,” Advanced Electronic Materials aelm.202300085 (2023). Chosen for the Back Cover of the Journal. Media Coverage: EurekAlert! (AAAS), Tech Xplore, Nanowerk, Purdue News.

Machine Learning Complexity in Quantum Materials

We have developed a new machine learning method that explains why electrons clump into strange patterns at the surface of so many quantum materials. The method, which uses the distribution of outputs from a convolutional neural network to estimate confidence, was able to accurately classify images of the surface of the quantum material vanadium dioxide (VO₂) and identify the factors that cause electrons to clump.

Rather than transitioning from insulator to metal all at once, VO₂ forms an intricate network of metallic puddles that extend like filigree over a wide range of temperatures. We developed a convolutional neural network to harvest information from both optical microscope and scanning near field optical images of the metallic filigree. The neural network was able to identify the factors that cause electrons to clump during the transition, such as interactions with defects in the material and the strength of the electron-electron interactions. This reveals that the intricate patterns share universal features with domain structures in magnets, stripe orientation fractals in superconductors, and antiferromagnetic domains in rare earth nickelates, pointing to a universal origin of electron clumping in quantum materials. This identification opens the door to using hysteresis effects to sculpt the filigree, in order to improve the function of VO₂ in novel electronic applications such as neuromorphic devices.

S. Basak, M. Alzate Banguero, L. Burzawa, F. Simmons, P. Salev, I. K. Schuller, M.M. Qazilbash, D. N. Basov, L. Aigouy, A. Zimmers, and E. W. Carlson, “Deep Learning Hamiltonians from Disordered Image Data in Quantum Materials,” Physical Review B 107, 205121 (2023). Media Coverage: EurekAlert! (AAAS), Phys.org, and Purdue News.

Superconductor is filled with Stripe Fractals

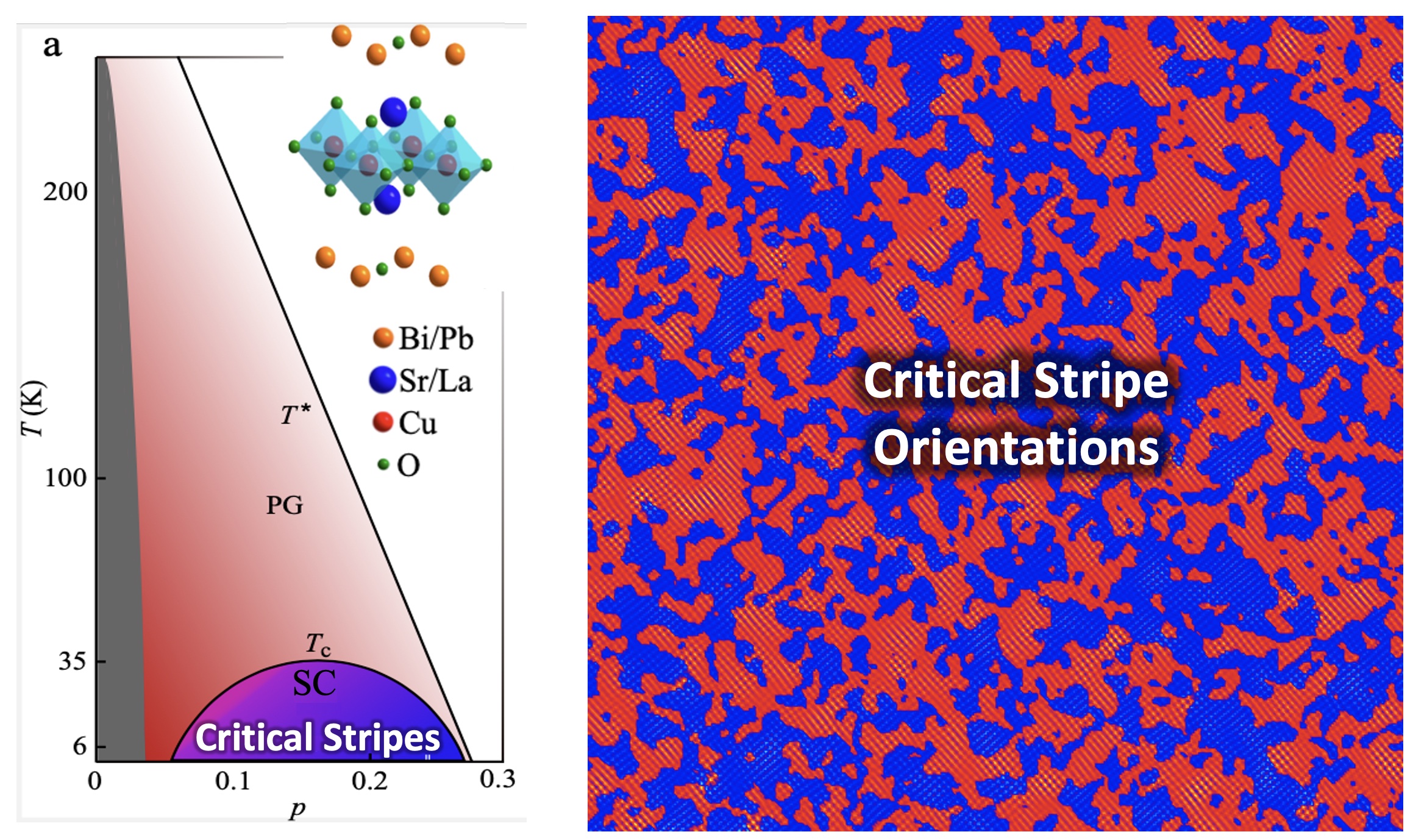
Scanning Tunneling Microscopy images of the surface of the high temperature cuprate superconductor BSCO reveal that electrons form stripes in which the local electron density oscillates from high to low. However, unlike a perfectly striped wallpaper, these images show that the stripes randomly change orientations from vertical to horizontal, as though someone ripped jagged edges into the stripey wallpaper and hung half of it as vertical stripes, and half of it as horizontal stripes. Using cluster techniques that we introduced to the field of quantum materials, we showed that these stripes form fractals. And rather than growing merely on the surface of the material, like frost on a window, these fractals are more like trees, whose roots reach deep underground. Moreover, the same fractal structures were observed throughout the superconducting doping range, far beyond the influence of a putative quantum critical wedge. We showed that these stripe fractals are driven not by quantum criticality, but by classical, disorder-driven criticality.

Cuprate superconductors are the highest known transition temperature superconductors that work at ambient pressure, and unlocking their secrets could lead to the development of superconductors that work at both ambient pressure and room temperature. Our discovery has important implications for developing higher temperature superconductors, since the changing orientations of the stripes disrupt insulating tendencies, favoring superconductivity.

C.-L. Song, E. J. Main, F. Simmons, S. Liu, B. Phillabaum, K. A. Dahmen, E. W. Hudson, J. E. Hoffman, E. W. Carlson, “ Critical Nematic Correlations Throughout the Superconducting Doping Range in BSCO,” Nature Communications 14, 2622 (2023). Media Coverage

Spatial Complexity in Strongly Correlated Electronic Systems

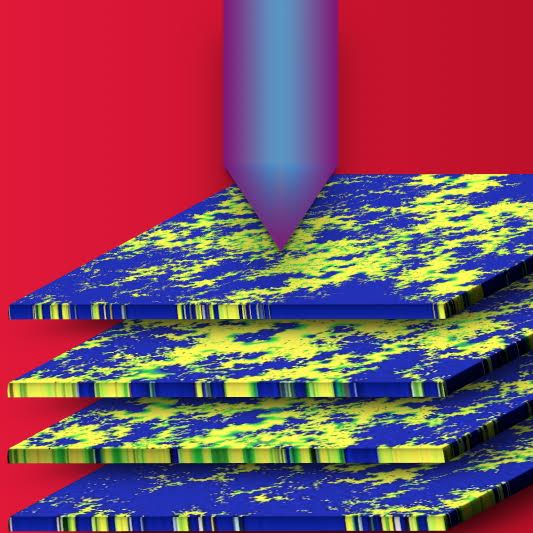
Inside the metals, semiconductors, and magnets of our everyday experience, electrons are uniformly distributed throughout the material. By contrast, electrons often form clumpy patterns inside of strongly correlated electronic systems (SCES) such as colossal magnetoresistance materials and high temperature superconductors. In copper-oxide based high temperature superconductors, scanning tunneling microscopy (STM) has detected an electron nematic on the surface of the material, in which the electrons form nanoscale structures which break the rotational symmetry of the host crystal. These structures may hold the key to unlocking the mystery of high temperature superconductivity in these materials, but only if the nematic also exists throughout the entire bulk of the material.

Using new methods we have developed for decoding these surface structures, we find that the nematic indeed persists throughout the bulk of the material. We furthermore find that the intricate pattern formation is set by a delicate balance between disorder, interactions, and material anisotropy, leading to a fractal nature of the cluster pattern. The methods we have developed can be extended to many other surface probes and materials, enabling surface probes to determine whether surface structures are confined only to the surface, or whether they extend throughout the material.

E. W. Carlson and K. A. Dahmen, "Using Disorder to Detect Locally Ordered Electron Nematics via Hysteresis," Nature Communications 2, 379 (2011).

S. Liu, B. Phillabaum, E. W. Carlson, K. A. Dahmen, N. S. Vidhyadhiraja, M. M. Qazilbash, and D. N. Basov, "Random Field Driven Spatial Complexity at the Mott Transition in VO2," Phys. Rev. Lett., 116, 036401 (2016).

High Temperature Superconductivity

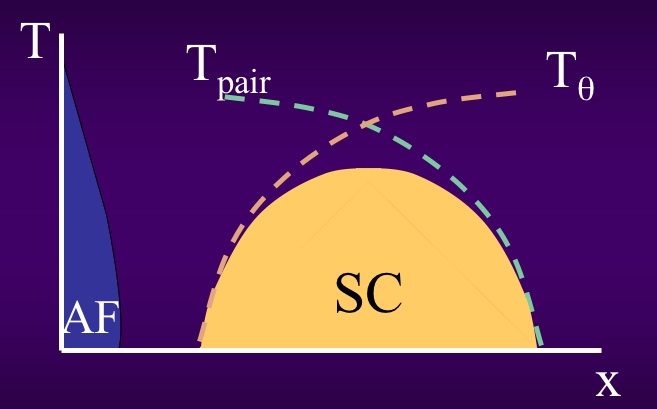
Superconductivity requires that electrons pair, and also become phase coherent. The transition temperature to superconductivity must be below both the energy scale of pairing, and the energy scale of phase coherence. The "catch 22" of raising the transition temperature is that raising one of these energy scales often results in the decrease of the other, and it is difficult to parametrically raise the transition temperature. This is seen empirically in the cuprate superconductors, where on the underdoped side, pairing (as measured by, e.g. the single particle tunneling gap) is strong but the phase stiffness energy scale (as measured by London penetration depth measurements) is weak. On the overdoped side, the situation is reversed, and as the phase stiffness energy scale rises, the paring scale is depressed.

E. W. Carlson, V. J. Emery, S. A. Kivelson, and D. Orgad, "Concepts in High Temperature Superconductivity," in The Physics of Conventional and Unconventional Superconductors, Vol. 2, ed. K.H. Bennemann and J.B. Ketterson (Springer-Verlag 2004)

Electronic Ising Nematic

Stripes within the copper-oxygen plane tend to lock to favorable lattice directions. For certain ranges of dopings, stripes lock to the Cu-O bond direction. In a four-fold symmetric crystal, stripes can lock either "vertically" or "horizontally" in the copper-oxygen plane, giving a natural mapping to the Ising model, where, e.g., up spins correspond to vertical stripe patches, and down spins correspond to horizontal ones. Disorder in the form of dopant atoms between planes favors one or the other direction locally, and acts as a random field on the Ising pseudospin. We are studying the consequences of this mapping for macroscopic nonequilibrium properties such as anisotropic transport, and also for local probes such as scanning tunneling microscopy.

E. W. Carlson, K. A. Dahmen, E. Fradkin, S. A. Kivelson, "Hysteresis and Noise from Electronic Nematicity in High Temperature Superconductors," Phys. Rev. Lett, 96, 097003 (2006).

Vortex Smectic-A

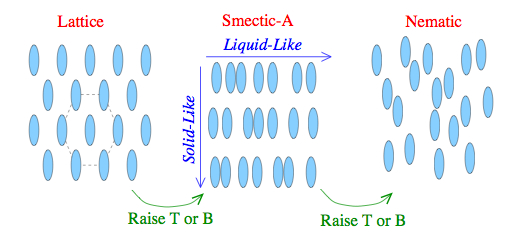
In anisotropic Type II superconductors, vortices have elongated cross sections, and anisotropic interactions. Anisotropic, repulsive objects generically give rise to liquid crystal phases. We predicted a new type of vortex phase in anisotropic superconductors, whereby the anisotropic Abrikosov lattice melts first into a smectic as temperature is raised, and then into the high temperature disordered phase. The vortex smectic forms an intermediate broken symmetry phase, where the vortices are liquid-like in one direction perpendicular to the external magnetic field, but lattice-like in the other. Because vortices melt first along the direction of short lattice constant, the intermediate phase has the symmetry of a smectic-A.

E. W. Carlson, A. H. Castro Neto, and D. K. Campbell, "Vortex Liquid Crystals in Anisotropic Type II Superconductors," Phys. Rev. Lett. 90, 087001 (2003).

Spin Waves in Striped Phases

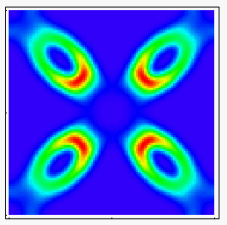
Certain nickelate materials and some cuprate materials show evidence of stripe phases, whereby holes doped into an antiferromagnet congregate in lines called charge stripes. Each charge stripe introduces a line defect in the form of a &pi phase shift in the parent antiferromagnetic texture, leading to the formation of spin stripes as well. The elementary excitations of fully ordered spin stripes are spin waves, observable as finite energy excitations in neutron scattering experiments. We have studied both site-centered stripes, where the charged domain walls like on Ni or Cu sites, and bond-centered stripes, where the charge lines lie between Ni or Cu sites, and developed a litmus test for ruling out site-centered stripes from low energy neutron data.

E. W. Carlson, D.-X. Yao, and D. K. Campbell, "Spin Waves in Striped Phases," Phys. Rev. B, 70, 064505 (2004).