Physics 271L Experiment 2

Equipotential Plotting

[ Theory | Apparatus | Procedure | Questions ]

 
Purpose: To locate experimentally some of the equipotentials in a conducting medium and to use these equipotentials to determine electric field lines.

Reference: Electrostatic potential, potential difference, electric lines of force, etc. are discussed in Halliday, Resnick and Krane, Chapters 28 and 30.

Supplies: You should bring white or graph paper, pencils, and a French curve if you have one.

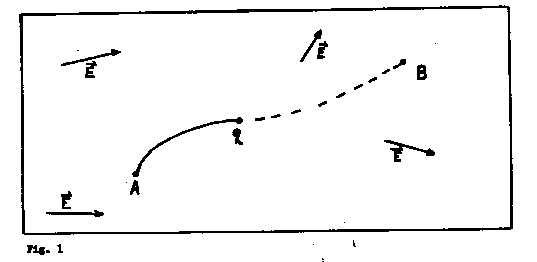
Theory: Suppose we have a region in which there exists a static electric field E which may vary in magnitude and direction from point to point (see Fig. 1). Also suppose we have a charge q initially at rest at point A and that we somehow "hook on" to q and put it to point B and leave it at rest there. ( We assume for simplicity that there are no friction forces and that the region is not in a gravitational field ) Then the electrostatic potential of point B with respect to point A is defined as the mechanical work done on q in going from A to B divided by q. In symbols,

(1)

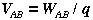
From elementary mechanics, have the usual expression for the mechanical work:

(2)
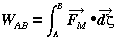
where 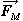is the net mechanical force at each point and 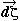is the usual line increment.

Now if q is to start from rest and end at rest there must be no net acceleration. One way of accomplishing this is to require the net mechanical force to balance the electrical force at each point along the path, that is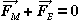
or
(3)
The electrical force on a charge q is given by 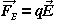, so
(4)
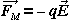
Substituting (4) into (2) and using the fact that q is constant we obtain
(5)
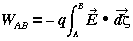
and finally, using (1),
(6)
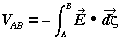
This is the basic equation for electrostatic potential differences. Notice that two points must be specified in computing V_AB ; to say that point B alone has a certain potential is meaningless. It will also be shown in lecture that for a given region and electric field V_AB depends only on points A and B and is independent of the path between them.

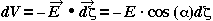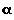Equation (6) may also be written in the differential form: where is the angle between 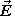and 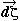. If we define, 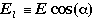the projection of 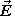along 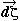, then
(7)

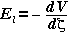
The quantity 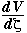, the change in potential with respect to change in distance along 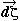, is called the "directional derivative".

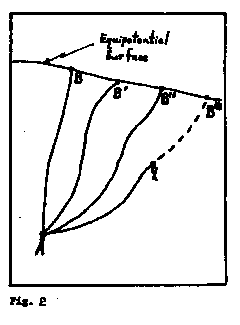
Now suppose we replace q at A and pull it along a different path until it reaches a point B' such that 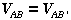. If we repeat this procedure many times we will find a set of points B, B', B'', . . . ., all of which have the same potential with respect to point A (See Fig. 2). This set of points defines an equipotential surface having the property that the potential difference between any two points on the surface is zero.

This property allows us to derive a relations between the direction of 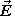and the equipotential surface. We have already shown that 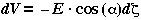, in general. If we stay on an equipotential surface then dV=0 so .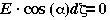

Since 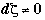and 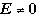in general, we must have 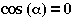. This occurs only if 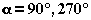. In other words 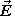is perpendicular to an equipotential surface.

Finally, suppose that for some region a series of equipotential surfaces have been determined such that the potential difference 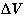between two adjacent surfaces is the same for all surfaces. We have shown that 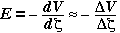, and since 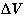is a constant then E is greatest in the area in which 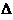z , the spacing between two adjacent surfaces, is least, and vice versa.

Apparatus: The region you will inspect is a sheet of graphite paper so you will be working
in two dimensions instead of three and will be finding equipotential lines instead of surfaces. The apparatus is shown pictorially and schematically in Figs. 3(a) and 3(b)

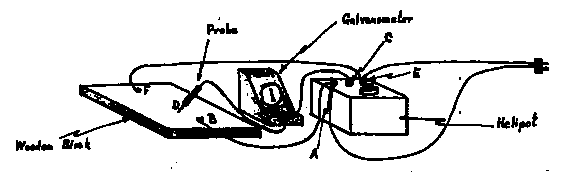
Fig3(a)

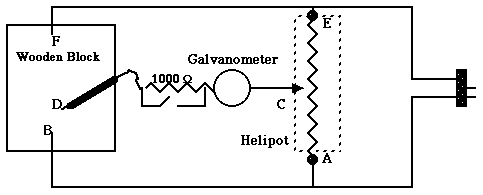
Fig3(b)

Points A and B are connected by a wire so there is no potential difference between them. By adjusting the dial of the helipot V_AC may take on any value from zero to V_AE , and by pressing the probe to different points on the graphite paper V_BD may take on any value from 0 to V_BF ( = V_AE  since EF and AB are connected by wires ). If C and D are placed so that there is potential difference between them ( 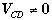means that 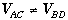) then the galvanometer needle will deflect. In this experiment you will set V_AC to known values and then adjust the probe position so that no galvanometer deflection is seen, indicating .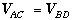

Procedure

1. Assemble a stack of papers as follows: bottom one sheet of white paper; next, one sheet of carbon (not graphite) paper; next, white; then carbon; and, on top the graphite paper with silver electrodes (choose the simpler pattern first).
   
   
2. Place this on the wooden block and press the paper down so that the terminals come up through the painted electrodes.
   
   
3. Trace the outline of the electrodes so they will be recorded on the white paper.
   
   
4. Assemble the apparatus as shown in Fig. 3(a) and 3(b) and have the instructor check the construction.
   
   
5. After circuit is okayed, set the helipot dial to 5.00 and plug in the apparatus (Socket A).
   
   
6. Holding the probe perpendicular, touch it to the graphite sheet near the center. (Press fairly firmly; there's a non-conducting paraffin film over the graphite and you must penetrate this).
   
   
7. If the galvanometer deflects, move the probe towards one of the electrodes slightly and note whether the deflection increases of decreases. Keep moving the probe until you get no deflection. Draw a small circle around this point on the sheet. (When moving the probe, lift off the paper. If you drag it along the sharp tip will cut the paper and change the equipotential pattern.)
   
   
8. Now move the probe ~1/2" - 1" towards one side of the paper and find another point which gives you a null reading.
   
   
9. Repeat this until you have a series of points from one side of the paper to the other. Look for points ~3/8" apart if the line is curving sharply and as you approach the edge of a conductor or the edge of the paper. Use 1" - 1 1/2" spacing if the line is not changing direction rapidly.
   
   
10. Now reset the helipot to 4.00 and repeat the procedure. Continue until you have lines for helipot settings of 1.00, 2.00, 3.00, 4.00, 5.00, 6.00, 7.00, 8.00, 9.00.
    
    
11. Remove the stack of papers from the board and have each partner take one of the white sheets, which should now have a series of dots and circles on them.
    
    
12. Assemble a new stack of papers using the second graphite sheet for the top.  Find the equipotential lines for this second sheet.
    
    
13. Remove the papers and unplug the apparatus. Using a French curve, if available, complete the lines through the points on all your white sheets. Note especially how the equipotentials lines behave when they are close to conductors.
    
    
14. To represent electric field lines start from one of the painted electrodes and draw a series of smooth curves to the other electrode, using the fact that electric field lines and equipotentials cross at right angles. Determine the direction of the electric field by observing the polarity of the electrodes. Again, notice how the electric field lines behave in the neighborhood of conductors and insulators. Also find areas in which the electric field is strong and those in which it is weak. How are these areas related to electrode position and shape?
    

Questions:

1. How many equipotential lines can pass through a conductor in a static electric field? Why?
   
   
2. Observe your data closely. What is the angle between the edge of the sheet and each equipotential line as it meets the edge? Can you explain this?
   
   
3. How do the characteristics of equipotentials in a limited two-dimensional region differ from those in an infinite three-dimensional region?
   
   
4. Can you use symmetry arguments to reduce the number of points you must take to determine equipotentials lines in some of your electrode patterns?
   
   
5. Observe your data closely. What is the angle between the edge of the conductors or electrodes and the electric field lines? Can you explain this?