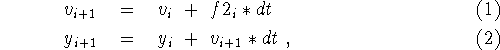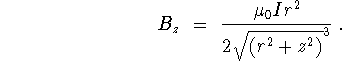
Note that the correct result (the one given here) was used to generate the solid curve in Figure 5.16. Thanks to Bob Delaney for finding this and the next several errors.
! x(i,n), y(i,n) = position of particle n ! i = 1 and 2 correspond to the old and current positions
The Euler-Cromer method can be written as
where ![]() is the second derivative of y at step i. This also implies
that
is the second derivative of y at step i. This also implies
that
![]()
The Verlet method can be written as
If one eliminates ![]() from (2) one arrives at
precisely (4). Hence, the two methods are equivalent
with regards to y.
from (2) one arrives at
precisely (4). Hence, the two methods are equivalent
with regards to y.
However, they are not necessarily the same with regards to the velocity. For the Verlet method it is best to obtain the velocity as a centered difference
![]()
which is different, and more accurate than, the Euler-Cromer expression.
Thanks to Sam Buss for pointing out the equivalence of the Euler-Cromer and Verlet methods.
! n = 1 = position two time steps ago
Thanks to Ramin Jamshidi for finding these errors.