Quantum Mechanics in Plain English
Quantum mechanics takes us into the wild and wacky world of the really small where particles are waves, waves are particles, and the physical intuition we have from our everyday life doesn't seem to work. If you and I lived in Quantumland, we could sit in three chairs at once and speed without getting a ticket. Sound like a nice place? Fasten your seatbelt for a quick tour.
Particles are Waves?
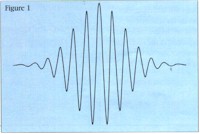
Quantum mechanics describes what the world looks like on scales as small as an atom or smaller. As it turns out, what we think of as particles, such as protons and electrons, can also be described as very tiny waves. The picture above shows an example. Where the wave is flat, there is no particle. The particle is somewhere in the wiggly part. (Exactly where? We'll get to that.)
The wave tells us more than where the particle is and is not. Where the wave wiggles indicates the particle's position. The shape of the wiggles reveals what the particle is doing (what its energy is, or its velocity, etc.). If we know where the particle is and what it is doing, we know just about everything about it, and we say we know its state. So the state of a particle is determined by the shape of the wave and tells everything about the particle. The wave always has a definite shape, and that's the fundamental truth about that particle.
Measurements, Part 1: How to Sit in Three Chairs at Once
The state of the particle is just whatever the particle is doing. Let's say the particle is sitting behind your couch; then it's in the "behind-the-couch state." If it's on the ceiling, it's in the "on-the-ceiling state." To find out something about the particle we ask it questions, such as, "Where are you?" In other words, we make measurements, but we can't measure the wave directly. The information to answer the question is in the particle's state. Grab hold of this axiom: Quantum mechanics says there are only certain allowable answers to our questions--much like a bad governmental form. Each allowable answer is a pure state corresponding to the question asked. For example, if we ask the particle where it is and it answers, "I'm behind the couch," we say it's in the "behind-the-couch" state. The answer, "I'm on the ceiling," corresponds to the "on-the-ceiling" state. These are examples of pure states of position.
If particles were always in pure states, quantum mechanics would be easy. The "behind-the-couch" particle could always reply, when we ask where it is, "I'm behind the couch." Unfortunately, particles are rarely that simple. Often they exist in mixed states. For example, the particle could be in a state that combines both the behind-the-couch and on-the-ceiling states. It could be in a state that's 30 percent couch and 70 percent ceiling.
But a problem arises when we ask the particle where it is. It cannot say, "I'm 30 percent of the way between the couch and the ceiling" because it is not somewhere in the middle. Rather, it is in both places at once. Imagine what the wave looks like. If the particle were in a pure couch state, its wave would be flat everywhere in the room except for the wiggly part behind the couch. If the particle were in a pure ceiling state, its wave would only wiggle on the ceiling. But since it's in a mixed state, we have a wiggly part behind the couch and a wiggly part on the ceiling. There's still just one particle, but its wave has two wiggly parts. It's in two places at once.
If you lived in Quantumland, you wouldn't have to choose where to sit in a movie theater--front, middle, or back. You could sit in all three places at once!
Measurements, Part 2: Observers Disturb What They Measure
Quantum mechanics says only certain answers are allowable. In the case of our pesky couch and ceiling particle, only "couch" or "ceiling" is an allowable answer. This is the crux of quantum mechanics: since the answer must be either "couch" or "ceiling," and cannot be somewhere in between, we say the answers are quantized. In other words, when we ask this mixed particle where it is, there is a 30% chance it will say "couch" and a 70% chance it will say "ceiling." And nobody has any control over which answer it will give. The particle does not know which answer it will give, and we, the askers, have no way of determining which answer the particle will give. The limitation here is not a limitation of our experiments or measurements. The particle itself doesn't know what it's going to say until it has already become that answer. This is by far the weirdest of all quantum phenomena.
Here's the situation. When a mixed particle is forced by our question to give us an allowable answer, it will suddenly and uncontrollably be thrown into a pure state of the type the question demands. When we ask the question, we force the particle into a pure state of that question type, but we have no way of knowing which state that will be. When the particle gives its answer, it becomes a pure state, and it will stay that way until otherwise disturbed. Let's say that when we asked the particle where it is, it replied (and was snapped into),"The couch state." That, of course, is a pure position state, not a mixture of two position states. It is true, though not the whole truth. We'll never know about the ceiling state, and the particle has no recollection of it. But from now on, if we ask it again where it is, the particle will always say it's behind the couch.
Remember the movie theater? You really could sit in three places at once. But, when someone asks you where you are sitting, you would suddenly be thrown into one and only one seat, say in the front, and "front" would have to be your answer, even though there's more truth to be known about where you used to be sitting.
Quantum Police and the Uncertainty Principle
What if we now asked the particle a different question? Instead of asking where it is we might ask how fast it's going. After all, it's already in a pure position state (behind the couch), it shouldn't have any choices left, right? Wrong. That pure position state may not be a pure velocity state. It might correspond to a pure velocity state, but then again it might correspond to a mixture of velocity states. (See how rascally particles can be?) In fact, quantum mechanics says that the position states are never the velocity states, and the velocity states are never the position states. Rather, one always corresponds to a very garbled mixture of the other kind: one position state is a mixture of an infinite number of velocity states, and a velocity state is a mixture of an infinite number of position states.
So, if the particle has told us it's behind the couch and we then ask it how fast it's going, there's no telling what answer we'll get. This is Heisenberg's uncertainty principle! Heisenberg's principle is usually stated this way: The more we know about where the particle is, the less we know about its momentum along that direction, and vice versa. (Heisenberg refers to 'momentum" rather than velocity" because momentum is directly related to how the wave curves.)
Let's say you are driving down the freeway in Quantumland, in a pure velocity state, at 80 mph. A quantum police officer could point a radar gun your way and measure your velocity. When the officer measures your velocity, it's as if he has just asked you how fast you are going. Since you're in a pure velocity state, the radar gun has a 100 percent chance of saying 80 mph. But remember, a pure velocity state corresponds to an infinite mixture of position states. Although the quantum officer knows exactly how fast you are going, he cannot find you to write you a ticket, because you're in an infinite number of places at once. There are no speeding tickets in Quantumland!
Confused? Join the Crowd
These are the essential ideas of quantum mechanics. If you find something in this article too preposterous to believe, you're in good company. At first even Einstein refused to believe that probabilities (percent chances) underlie quantum mechanics. Crazy ideas such as this one take awhile for anyone to digest. But keep in mind Faraday's words: "Nothing is too wonderful to be true."
This article © 1997 originally published at Reasons To Believe.
Reprinted with permission.


