Reference: Louis Lyons, A Practical Guide To Data Analysis For Physical Science Students, Cambridge Univ. Press, 1991.
In many of the experiments you will be expected to graph data and extract information
from the graph. The following discussion and exercises are intended to give you a view of
basic graphing practices and an introduction to techniques which obtain information by
graphing. Several computer analysis codes which extract detailed information from
graphical representations of data are now available.
Although a graph of raw experimental data is often used to suggest the dependence of the y-variable
on the x-variable, in most instances this semester you will already know the
dependence and will be trying to determine the various constants in the descriptive
equation. Your first step then is to make a change of variables such that the graph is
linear, of the form
![]() .
.
For example if you know that x and y are related as
![]() ,
,
then the appropriate change of variable would be
![]() .
.
Graphing y versus u would yield a straight line with the
slope = A and a y intercept = B.
When you have decided on the appropriate change of variables, you should make a table of
the original data with columns added for the newly defined variables. Continuing with the
example above a typical table would be:
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| y | 4 | 7 | 28 | 85 | 196 | 379 |
| u3 | 0 | 1 | 8 | 27 | 64 | 125 |
Now that you know the range and domain of the function you should choose an appropriate
scale. The scale should fit the rulings of the graph paper naturally in order to avoid
errors in placing the points. It should be expanded enough to show the form of the line,
but not so expanded that the scatter of points confuses the general shape.
Once the scale is chosen, you should label the axes, including units, and
enter the data points. If you have correctly chosen the change of variables, the points
should lie along a straight line. However, because of the experimental error associated
with the data, the points will scatter about a line with the amount of scatter dependent
upon the errors involved. By including error flags on the points, you can decide whether a
linear representation is justified. The error flags are usually vertical (and/or
horizontal) lines drawn through the data points with lengths corresponding to the
estimated errors i.e.
![]()
The line which fits the data should intersect most of the error flags.
Figure 1 is an illustration of how different sizes of error flags require different curves
to represent the data. Errors of ± 0.7 are shown for each point in Figure 1a, whereas the points in Figure 1b each have error flags of ± 0.2. In the first
figure a the solid straight line provides a good fit to the data; in contrast the dashed
line does not. Points in the second figure have smaller error flags and are not well
described by a line. The curve shown is a polynomial fit to the data ( 7th order).
When you have finally achieved a straight line graph, the next step is to determine the
slope and intercept which completely characterize the line. The intercept is the value of y
at x=0; intercept = y(0), including the units. It should be
noted that the y-axis is not always located at x=0; check your scale.
To determine the slope, find two points on the straight line which is fitted to the data (
do not use experimental points, even if they fall on the line ). Draw a vertical line down
from the upper point and a horizontal line from the lower point to form a triangle.
Indicate the changes in x and y as
respectively, on the appropriate sides of the triangle. The slope m is determined by
m = D y / D x
including units.
As an exercise, you should graph the data in the exercises 1 through 4 in such a
manner that straight lines will result. From these graphs, calculate the slopes and
intercepts that specify the linear relationship. Use the graphs drawn for the
calculations, not the data points. Example A is provided as an illustration of the method.
These graphs and the exercise #4 constitute the written report for the first experiment.
Example A: The intensity of a beam of X-rays after passing
through an absorber of thickness x is given by:
![]()
where e is the base of the natural logarithms and Iois the
intensity of the beam at the surface of impact. From the following data, change variables
to obtain a linear plot and determine the constants Io and µ
from the plot.
Data: Here r indicates the units of intensity, say counts/second.
| I(r) | 2.43 | 1.47 | .893 | .541 | .328 | .199 | .121 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x(mm) | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 |
Analysis: First rewrite the equation as:
![]()
and add the values of lnI to the table.
| lnI(r) | .888 | .385 | -.113 | -.614 | -1.11 | -1.61 | -2.11 | |
|---|---|---|---|---|---|---|---|---|
The values of ln I are then plotted as a funtion of x , shown in
the following figure:

Using the indicated triangle ABC, the slope -µ = (-2 -1.39)/6.8 = -0.50/mm
or
µ = 0.50/mm. Extrapolating across the ordinate, ln Io=
1.39 giving Io = 4.0 (rate, say counts/second)
![]()
Plot the following data to obtain a linear graph and determine A and B.

![]()
Plot a linear graph using functions C1and C2and determine C from the following table:
| C1(mF) | 32 | 41 | 55 | 70 | 93 |
| C2(mF) | 115 | 66 | 46 | 39 | 34 |
3. An AC circuit containing resistance R and inductance L has a current amplitude given by:
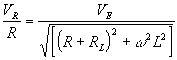
For a constant VE=
2.5 volts and R = 10.0 ohms, varying the angular frequency
![]() gives the
following values of VR Make a linear plot from which L and
RLmay be found.
gives the
following values of VR Make a linear plot from which L and
RLmay be found.
| w(s-1) | 600 | 900 | 1200 | 1500 | 1800 |
| VR(volts) | 1.24 | 1.12 | 0.98 | 0.87 | 0.77 |
4. A radioactive sample containing No
atoms decays according to the relation
N=N0exp(-t /t)
where N is the number of atoms remaining after a time t, and t is the time constant for decay. Data can be obtained for the rate of decay dN/dt at anytime t. The following table gives these data with estimates of the precision of dN/dt at each point. Make a linear plot using these data and determine No and t from the plot. Show error bars and from them calculate the precision to which this data gives the values of No and t
| t (sec) | -dN/dt |
| 0 | 110± 4% |
| 1.30 x103 | 100± 4% |
| 2.60 x103 | 85± 4% |
| 6.50 x103 | 66± 4% |
| 10.4 x103 | 50± 4% |
| 13.0 x103 | 38± 4% |
| 26.0 x103 | 14± 4% |
| 39.0 x103 | 5± 4% |
| 52.0 x103 | 2± 4% |
.