Errata/Comments for
Computational Physics, 2nd Edition
- In Example 2.2 on p.27, on the right of the two
equations for computing the air drag force, the terms (B2/m)
should read B2. Thus the equations should have been:
Fdrag,x = - B2 v vx,i, Fdrag,y = - B2 v vy,i
We appreciate the help by Jeff de Jong for finding this and a few other errors.
- On p.22, as noted in footnote 5, the definition of the
drag coefficient C was changed by a factor of 2 from the first
edition of this book (cf. Eq.(2.9)). This actually
corrected an implicit error in that edition in presenting the measured
values of C in Figure 2.6 as well as to conform better to the
standard definition. On the other hand, in section 2.5 on Golf, we
continued to use the old definition of C in Eq.(2.34).
Thus the discussion of numerical values of C in section 2.5
corresponds to half of the values of the drag coefficient in the analogous
discussion on the baseball in previous sections. This invites confusion
and we regret that we had not unified the definition of C in all
sections. Thank you for Jeff de Jong for raising this issue.
In addition, Charles Maguire pointed out that the caption of Figure 2.2 on p.23 quotes an incorrect value of the drag coefficient; while it states C=0.5 was used, it should have been C=1 instead according to the new definition in this edition of the book.
- On p.48, just preceeding Eq.(3.1), we state that "The parallel forces add
to zero, since we assume that the string doesn't stretch or break".
This is incorrect except at the highest points of the pendulum where its
velocity is zero since the net parallel force must provide the needed
centripetal acceleration to keep the pendulum in motion along a circular
arc. We thank John Goff and William DeBuvitz for
alerting us to this error.
- On p.49, 4th line from the top, "where l is
the length of the string" should be changed to "where l
is the length of the string and
 is measured in radians. (Pointed out by William DeBuvitz.)
is measured in radians. (Pointed out by William DeBuvitz.) - In Example 3.3 on p.58, there are 2 typos in the signs
for the time evolution equation for
 .
The minus sign in front of the bracket should be a plus and there needs to
be a minus within the brackets in front of the term (g/l) sin
.
The minus sign in front of the bracket should be a plus and there needs to
be a minus within the brackets in front of the term (g/l) sin  i. Thus, the corrected
equation should read:
i. Thus, the corrected
equation should read:
![]() i+1 =
i+1 = ![]() i + [- (g/l) sin
i + [- (g/l) sin ![]() i
- q
i
- q ![]() i + FD sin
(
i + FD sin
(![]() D ti) ]
D ti) ] ![]() t
t
We are grateful to Denis Donnelly for pointing this out.
- On p.98, the last row of Table 4.1 gives an incorrect
value for the mass of Pluto. It should read 1.3
 1022
kg. We
appreciate the help by Charles Maguire on this point.
1022
kg. We
appreciate the help by Charles Maguire on this point. - On p.125, in the expression for the moment of inertia I
just after Eq.(4.23), |r1| and |r2|
are meant to be the distances from the center of mass of the two particles
to each of the particles (and not from Saturn at the origin). This
notation was at best unclear as John Goff pointed out. This part should
have read
where I = m1d12 + m2d22 is the moment of inertia and the distances d1 and d2 are measured from the center of mass of the two particles to each particle.
- On p.131, line 6 from top and paragraph 2, line 5 and
again on p.138, paragraph 3, line 2, we refer to Fig. 12.47 where we
should have referred to Fig. 5.1 instead.
We have no idea why this happened and since there is a totally unrelated
Fig. 12.47 later on, it is a confusing error. We thank Gus Hart again for
spotting this problem.
- On line 3 and the last line on p.193, references
to Table 7.3 appear. The references should be Table 7.1 on the same page
instead.
- In Eq. (7.11) on p.194,
the equal sign (=) should be the proportionality sign (∝). This is because
the first step has 4 choices on the square lattice even though all later
attempts will have only 3 choices (by inhibition of the immediate back
tracking).
- In Eq.(7.20) on p.196, there
should be a factor of D on the right-hand side of the equation. Thank you,
Geron Bindseil for
bringing this to our attention.
- On p.220, The text that appear in the 2nd tertiary
bullet (dark dot) of Example 7.4 should have been enclosed within a box.
- On p.221, just above Example 7.5, the reference to
"the box in Example 7.8" should have been to "the box in
Example 7.4". This is the text that should have appeared within a box
but didn't (see above). Thanks to Bernhard Gubanka
for noticing this error.
- On p.225, just after Example 7.6, the reference to the
Depth-first algorithm described in "Example 7.3" should have
been to "Example 7.2".
- On p.229, at the beginning of the last paragraph,
"Another consequence effect of ..." should read "Another
consequence of ..."
- On p.265, just after Eq.(8.32),
the equation defining t that appears in Eq.(8.32) should have read t
 1 - zJ/kBT
1 - zJ/kBT
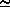 (T-Tc)/Tc. In other words, the
equality should have been an approximate equality since we have replaced T
in the denominator by Tc where T is near Tc.
This has been pointed out by John Goff. (Please note that we have defined t here as the coefficient of the term linear in
m in Eq.(8.32) that came from Eq.(8.31),
and thus did not define it as (T-Tc)/Tc as
might be more commonly done. Of course, the two expressions are nearly
equal near the critical point anyway.)
(T-Tc)/Tc. In other words, the
equality should have been an approximate equality since we have replaced T
in the denominator by Tc where T is near Tc.
This has been pointed out by John Goff. (Please note that we have defined t here as the coefficient of the term linear in
m in Eq.(8.32) that came from Eq.(8.31),
and thus did not define it as (T-Tc)/Tc as
might be more commonly done. Of course, the two expressions are nearly
equal near the critical point anyway.) - On p.274, in the 3rd line from bottom, the reduced unit
of time for Ar is given as 1.8
 10-12 sec,
but it should have been 2.2
10-12 sec,
but it should have been 2.2 10-12
sec instead. This is one of the many errors pointed out by Bernhard Gubanka.
10-12
sec instead. This is one of the many errors pointed out by Bernhard Gubanka. - On p.280, in Eq.(9.9), v2/kBT should be replaced by v/kBT. The prefactor of the exponential in d-dimensions
generally is proportional to vd-1 (kBT)-d/2.
Also, Eq.(9.10) is the correct distribution of
the x-component of the velocity in any dimensions. There, you
simply disregard the values of the other component(s) and just look at how
vx is distributed between negative
infinity and positive infinity; then you get (9.10). We thank Charles
Maguire for making us aware of the issues with these equations.
- In Eq.(9.17) on p.296, the two
factors of (
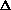 t)2
in the denominators should both be in the respective numerator. We are
grateful to Gus Hart for pointing out this error. Thus the corrected
equation should read:
t)2
in the denominators should both be in the respective numerator. We are
grateful to Gus Hart for pointing out this error. Thus the corrected
equation should read:
xi(n+1) = 2 xi(n) - xi(n-1)
+ (![]() t)2
[ xi+1(n) + xi-1(n) - 2 xi(n)
] +
t)2
[ xi+1(n) + xi-1(n) - 2 xi(n)
] + ![]() (
(![]() t)2 ( [ xi+1(n) - xi(n)
]3 + [xi-1(n) - xi(n) ]3 )
t)2 ( [ xi+1(n) - xi(n)
]3 + [xi-1(n) - xi(n) ]3 )
- There is a typo in the second bullet of Example 10.1 on
p.311. The initial values of
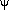 should be non-zero. That is, we should have
should be non-zero. That is, we should have 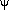 0 =
0 = 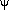 -1 = 1, e.g., and not 0. We are grateful to Katie
Sweet for pointing out this error.
-1 = 1, e.g., and not 0. We are grateful to Katie
Sweet for pointing out this error. - On p.317, in Fig. 10.8, we stated that the solutions
from left and right match fairly well for E=-1.969. While they do match
better for this energy than for E=-1.6, the error is still substantial.
Much better match is obtained for about E=-1.890, and thus the latter vaule would be an acceptable solution, but not
E=-1.969. Again, thank you, Bernhard Gubanka.
- On p.327, third line from the top, the reference to Eq.(10.17) should have been to Eq.(10.18) as φ
is a proposed solution for the Hamiltonian (10.17) and not of
it. Rather, it is a poposed solution of (10.18).
Thanks to Olle Windelius
for pointing this out.
- There is a typo in Eq.(10.41)
on p.335 pointed out by several readers (including Trevor Byrne). The last
term on the right should have a plus sign in front, not the minus. The
corrected equation should read:
R(x,t+![]() t)
t) ![]() R(x,t)
- [
R(x,t)
- [![]() t/2(
t/2(![]() x)2] [ I(x+
x)2] [ I(x+![]() x,t+
x,t+![]() t/2) - 2 I(x,t+
t/2) - 2 I(x,t+![]() t/2) + I(x-
t/2) + I(x-![]() x,t+
x,t+![]() t/2) ] +
(
t/2) ] +
(![]() t) V(x) I(x,t+
t) V(x) I(x,t+![]() t/2)
t/2)
- On p.339, the calculation for the Fig. 10.17 was
performed using the Crank-Nicholson method (rather than the leap-frog
method) and this should have been mentioned for clarity as the stability
conditions are different for the two methods.
- On p.345, there is a typo in Eq.(10.56)
pointed out by Elie Kawerk.
On the last line of the equation, in the numerator, the term R(x,y+
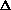 x,t) should have been R(x,y+
x,t) should have been R(x,y+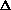 y,t). Also note, as stated at the top of p.346, we have
already set
y,t). Also note, as stated at the top of p.346, we have
already set 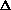 x=
x=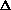 y on that line to get
the denominator to be (
y on that line to get
the denominator to be (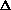 x)2.
x)2.
- On p.384, the second line of Eq.(11.31)
should read:
p(i,n+1) = p(i,n) - ...
that is, the second index of p(,) on the right had side should be n instead of n-1.
- On p.440, in the second line of Eq.(12.23)
the exponent -V/20 should read -V/80. That is, that line
should be
![]() n = 0.125 e-V/80
.
n = 0.125 e-V/80
.
- This is not an error per se, but in Appendix A.3, we
discuss the Verlet method and its local error of
O[(
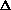 t)4].
Gus Hart has made a rather interesting observation that the application of
the Verlet method to the exactly solvable
problem of the simple harmonic oscillator produces a cumulative error of
O[(
t)4].
Gus Hart has made a rather interesting observation that the application of
the Verlet method to the exactly solvable
problem of the simple harmonic oscillator produces a cumulative error of
O[(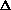 t)2]
rahter than the naively expected one of O[(
t)2]
rahter than the naively expected one of O[(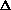 t)3]. This
turns out to be true also for the radioactive decay problem. There are
some arguments we could make for this unexpected behavior as a general
result (under certain assumptions) due to the faster accumulation of the
local errors by virtue of the way Verlet time
evolution works (A.19). So the analysis has an interesting twist that
neither author was aware of. This point will be further investigated and
may possibly be incorporated in a future edition.
t)3]. This
turns out to be true also for the radioactive decay problem. There are
some arguments we could make for this unexpected behavior as a general
result (under certain assumptions) due to the faster accumulation of the
local errors by virtue of the way Verlet time
evolution works (A.19). So the analysis has an interesting twist that
neither author was aware of. This point will be further investigated and
may possibly be incorporated in a future edition. - In Appendix B.2 on p.472, there are some typos. First,
on the 5th line of B.2, "x1 < x2 < x3"
should read "xa < xb < xc". Second, in Example
B.1, in the 3rd bullet, "g(x0)
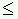 g(x1)"
should read "g(x0)
g(x1)"
should read "g(x0) 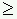 g(x1)". This error was pointed out by
Jeff de Jong.
g(x1)". This error was pointed out by
Jeff de Jong. - In Appendix C.1 on p.480, lines 1 and 2, "sines of
cosines" should read "sines and
cosines".
- In Appendix C.4 on p.488, line 2, the refernce to Fig. A2.4 should be one to Fig. C.4 instead. This and the previous errors were
pointed out by Gus Hart (as were many others).
- On p.490, there are two embarassing
errors. In Eq.(C.13), the integration is over t,
not
 . So d
. So d should be replaced by dt. In Eq.(C.14), the integral should be double, over both t
and τ. So there should have
been an inner (or outer) integral
should be replaced by dt. In Eq.(C.14), the integral should be double, over both t
and τ. So there should have
been an inner (or outer) integral 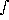 -
-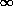
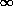 ... dt
on the righthand side. These errors were
discovered by Bernhard Gubanka.
... dt
on the righthand side. These errors were
discovered by Bernhard Gubanka. - About midway down on p.498, the equation that footnote
6 should be referencing is (D.18) but it appears as (??). Thanks, Len Finegold for pointing this out.
- On p.502, in Eq.(E.9), a
factor of
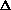 x
is missing on both terms on the right as pointed out by Dr. Anselmo.
x
is missing on both terms on the right as pointed out by Dr. Anselmo. - On p.510, lines 8 through 12 should be corrected. The
original statements were not taking proper account of a factor of the
panel size in multiple dimensional integration. Correctly taking account
of this, the leading order cumulative error is still N-1/d, N-2/d,
N-4/d for the rectangular panel, trapezoidal, and
Simpson’s rule integration just as in integration in one of the d-dimensions. The small errors just
add in more dimensions (not multiply). Thus, these methods do not become
“of no use”, but simply become less competitive against
methods such as Monte Carlo integration in higher dimension, which has N-1/2
error in any dimension.
- On p.518, in Eq.(F.4), a minus
sign is missing in the exponent.
- On p.527, in the 5th line from top, "was also
be" should read "can also be".
- Equations (H.4) and (H.5) in Appendix H on p.528 have
misprints. The last terms on the left-hand side of these equations should
be a1NxN and a2NxN, respectively. The "xN" in these terms were erroneously
shown as "x1" and "x2",
respectively, in the published version.
- On p.534, just after Eq.(H.27),
A x = f should be replaced by A x = b. On the
same page, just after Eq.(H.30), E(n)
should be replaced by En
(i.e., E raised to the n-th power).