MOTION OF A BATTED BASEBALL

Projectile motion is a topic used to illustrate many basic ideas connected with Newton's second law. A common approach is to consider the motion of an object which is dropped from a cliff, or thrown from a bridge, etc. The usual treatments of such problems completely ignore the drag force due to the air. In fact, students are often led to believe that it is not very important. However, it is easy to show that this is wrong. For example, consider a batted baseball hit as a high fly ball. Such balls are often hit with an initial speed of about 100 miles per hour. If a ball is hit vertically with this speed, the (calculated) time spent in the air ignoring air drag is about 10 seconds. If this were true, a typical outfielder would be able to run about 90 m during this time. Given the size of a typical baseball stadium, then if this were really true, the catcher would be able to catch many fly balls hit to the outfield! Of course, this is not the case; the moral here is that air drag plays a very important role.

Projectile problems involving realistic air drag are found in many areas of sports, including bicycle racing, baseball, and golf. These problems are described by ordinary differential equations in which initial values are given, and all can be solved with the Euler method (of course, more advanced methods work well too). They are good examples of interesting physics which can't be solved analytically, but can be easily tackled with a computer.

Here we will give an introduction to some of the physics which is important for understanding the motion of a batted baseball. Our goal is to understand how far a real baseball should be expected to travel when hit by a ``typical'' power hitter. The most important ingredient in our model will be the effect of atmospheric drag, and we will employ a fairly realistic model of this drag force.

It is interesting to begin by estimating how far a baseball would travel in a vacuum, that is, without atmospheric drag. This range can be calculated, either analytically, or numerically. A good power hitter can give the ball an initial speed of about 110 mph (49 m/s), and if it is hit at an initial angle of 45 degrees starting from a height of 1 m, the range in a vacuum would be 248 m, or approximately 815 feet. So far as I know, no one has ever hit a baseball that far. A typical outfield fence is 350-400 feet from home plate, and from practical experience we know that a 500 foot home run is an exceptionally long one. Thus, it is clear that baseball in a vacuum would a very different game than the one we are used to watching.

The drag force on an object which moves through a fluid is mentioned in virtually all introductory mechanics texts, which usually discuss the result for viscous drag as calculated by Stokes nearly 150 years ago. These texts then go on to introduce concepts such as the terminal velocity of a skydiver, etc. However, it turns out that the viscous drag force calculated by Stokes is of essentially no consequence for baseballs. Stokes' viscous drag force varies as the first power of the velocity of the object, but there is also a contribution to the drag which has a more complicated dependence on the velocity (it varies as the square of the velocity at low velocities). This latter contribution arises from the kinetic energy imparted to the fluid (in this case air) by the moving object. This ``quadratic'' contribution is much larger than the viscous drag for objects which move at any reasonable speed.

The book gives a discussion of this force, and shows how it varies with velocity. A calculation of the range of a batted ball with the proper drag force requires a numerical approach, since the force is not a simple function of the velocity. When this is done, one finds results like those given in the figure. Recalling that the range in a vacuum would be about 250 m, we see that air resistance has an enormous effect. The range of our power hitter is now approximately 120 m, or about 395 feet, which is in much better accord with the size of typical major league ballparks. The trajectory is also seen to be noticeably non-parabolic (in a vacuum it would be an exact parabola), which is also in agreement with our everyday experience.

  
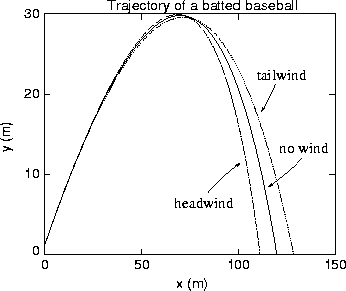
Figure: Calculated trajectory of a baseball hit at an initial velocity of 110 mph, with the effects of atmospheric drag included. Solid curve : no wind; dotted and dot-dashed curves: for a tailwind and headwind of 10 mph. In all cases we assume that the initial velocity makes an angle of 35 degreees with the horizontal.

The effect of the wind can be added to the calculation, and some results for a tailwind and headwind are also shown in the figure. It is interesting that major league parks are oriented so that the generally prevailing westerly breeze, which averages about 5 mph in the United States, is at the batter's back and thus favors a home run. As in most sports, offense is favored over defense; that is, the hitter over the pitcher.

It is also interesting to consider the effect of altitude. One finds that for the highest major league park (in Denver), a long fly ball will travel about 31 feet farther there than at sea level. The next highest major league park is in Atlanta (altitude 1000 feet), and here the effect of the altitude is to add about 6 feet to the range. In addition, the variation of the drag force with velocity is the key to understanding the motion of a knuckleball, but that is another story that we will not get into here (see the book for details).